In the last two articles, we talked about limits and their application in determining the continuity of a function. Here, we will apply those skills to few practice questions.
Attempt the problems on your own at first; however, if you get stuck, the solution to each problem is just below it. These problems vaguely range from easy to hard. Enjoy!

#1 Use the graph below of f(x) to answer the questions.

Solutions:
a) The “+” superscript next to the 2 tells us that we are looking at the limit as x approaches 2 from the right of f(x). Looking at our graph, our function f(x) gets super close to a value of 0 when x approaches 2 from the right.
b) Similarly, we are looking at the limit as x approaches 2 of f(x), but this time it’s from the left. Looking at the graph above, we see that f(x) gets super close to a value of 0 when x approaches 2 from the left.
c) Yes! Notice that our left- and right- sided limits are equal. Remember that if two one-sided limits of a function at some x-value exist and are equal, we can say that our overall limit exists and is equal to the same value as both one-sided limits.
d) Looking at the graph, f(2) = 0. Make sure that you did not use limits to find this value — recall that the limit as x approaches some c of f(x) does not necessarily equal f(c).
e) The function is certainly continuous at x = 2. One might look at the graph given and intuitively decide that it is continuous at x = 2. However, we should prove this assertion, for what if we weren’t given a graph but rather an equation?
First let’s think back to what our criteria for determining continuity at a point was:
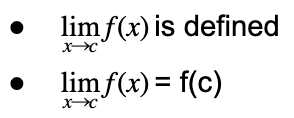
Note: f(c) should be defined, but I generally do not include that in my definition, because I feel as if it is pretty intuitive. However, you will see that some people do include that as part of the criteria for determining continuity.
We have already established that our two-sided limit is defined and that f(c) is defined. Now we only need to make sure that they are equal to each other. We found in part (c) that the limit as x approaches 2 of f(x) equals 0 and that f(2) equals 0 as well. Since these are equal, we have satisfied all the conditions for continuity at a point; thus, our function is continuous at x = 2.
f) For a function to be continuous on an interval, it must be continuous on every point in that interval. We already determined that f(x) is continuous at x = 2, and we can do the same thing for all the other points on [-2, 3], but…
Yikes. That’s a lot of points — in fact that an infinite number of points! But, if we think about the points in general, we can make this a little easier. Clearly the limit as x approaches each point in [-2, 3] is defined and f(x) is defined for every point in the interval. Additionally, it is pretty obvious from the graph that the limit as x approaches some value c on the interval is equal to f(c). So, each point on [-2, 3] satisfies the criteria of continuity at a point, and our function is indeed continuous on the entire interval.
Generally, you can determine whether a function is continuous just by looking at its graph and ensuring that there are no gaps or discontinuities present.
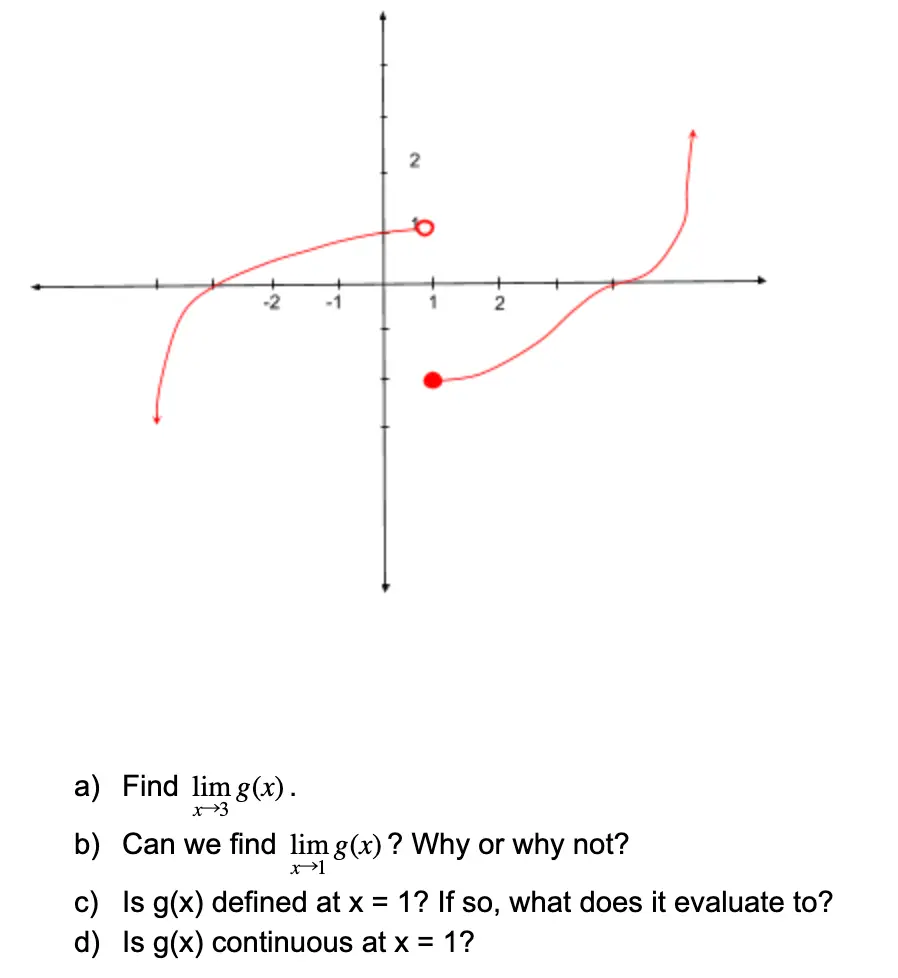
#2 Use the graph below of g(x) to answer the questions.
Solutions:
a) First, we make sure that the left-handed and right-handed limits are the same. This is true, as both single-sided limits at x = 3 are equal to -1. Thus, our overall limit is equal to that same value.
b) Without paying much attention, one might glance at the graph and notice “Hey, both one-sided limits at x = 1 are defined, so our limit must exist!” Be careful! The question asks for the overall two-sided limit at x = 1, not the one-sided limits. For a two-sided limit to exist, we must not only have both one-sided limits exist, they must also be equal to each other! This is definitely not the case for g(x), so we cannot evaluate our double-sided limit. We can express this by saying “The limit as x approaches 1 of g(x) does not exist.”
“Does not exist” is commonly abbreviated as “DNE” in writing.
c) Looking at the graph, we can determine that g(1) is indeed defined and is equal to -2. Be careful not to say g(1) = 1 — even though the left-sided limit of g(x) at x = 1 approaches a y-value of 1, notice that there is an open circle at (1, 1). The closed circle is at (1, -2) so our y-value for g(1) is -2. Had there been an open circle at (1, -2) as well, we would say that g(x) is not defined for x = 1.
d) In part b, we established that the limit as x approaches 1 of g(x) does not exist. Thus, our criteria for continuity is violated, namely that the double-sided limit must be defined. So, we can confidently say that g(x) is not continuous at x = 1.
#3 Use the function h(x) = 1/(x2) to answer the following questions.
Solutions:
a) There are a couple of ways to go about doing this. The first way is to think about this intuitively. As x approaches 0 from the right (or from the positive side), what happens to h(x) = 1/(x2)? Well, the x2 term gets smaller and smaller, getting very very close to 0 but not exactly reaching it. As a result, 1/(x2) blows up to a huge number and just gets larger as x gets closer to 0.
Another way would be to look at a table of x- and y- values, choosing x-values that get closer and closer to 0 from the right. You will once again notice that h(x) begins to grow very quickly in the positive direction.
Finally, you could also look at a graph of h(x) and visualize the limit. It would look something like:
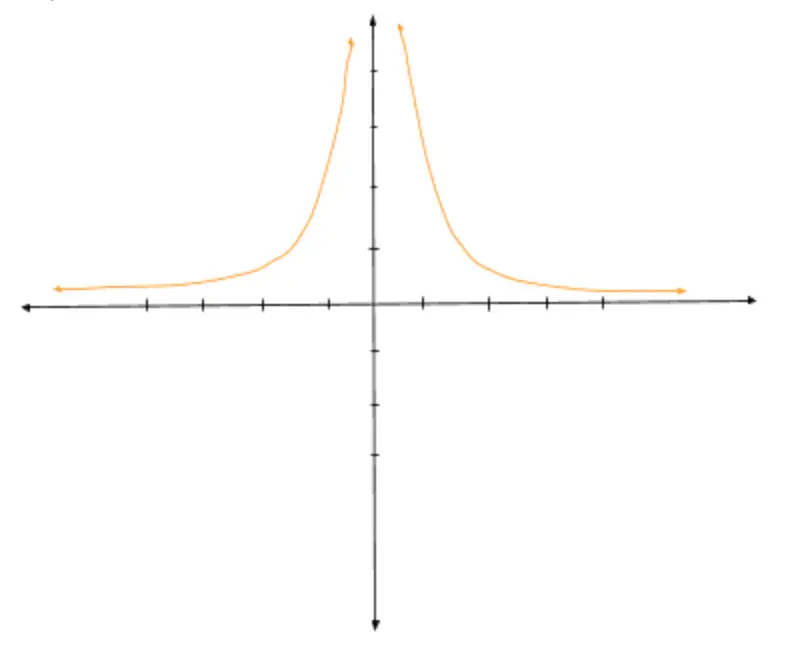
So our limit as x approaches 0 from the right of h(x) is infinity.
b) Using one of the methods in part a, we determine that the limit as x approaches 0 from the left of h(x) is also infinity. Make sure you understand why it is not negative infinity.
c) Though our limits imply that h(0) would be infinity, we cannot actually evaluate h(0). Saying h(0) equals infinity would not be mathematically correct, as “infinity” is not a finite value that h(x) achieves at x = 0. Instead, h(x) is not defined at x = 0, and we have a vertical asymptote instead (remember this from algebra 2?).
Works cited
https://socratic.org/questions/what-are-the-three-conditions-for-continuity-at-a-point
http://www.milefoot.com/math/calculus/limits/Continuity06.htm
https://unit8limits.weebly.com/two–sided-limits.html
https://www.expii.com/t/two-sided-limits-from-graphs-9972
http://www.milefoot.com/math/calculus/limits/Continuity06.htm
http://www.themathpage.com/aCalc/infinity.htm
Click and check out these popular articles for more information: 🙂
Calculus: Two Important Theorems – The Squeeze Theorem and Intermediate Value Theorem
Calculus: Limits and Continuity
Ectoderm vs Endoderm vs Mesoderm
Circulatory System: Blood Flow Pathway Through the Heart
Circulatory System: Heart Structures and Functions
Ductus Arteriosus Vs Ductus Venosus Vs Foramen Ovale: Fetal Heart Circulation
Cardiac Arrhythmias: Definition, Types, Symptoms, and Prevention
Upper Vs Lower Respiratory System: Upper vs Lower Respiratory Tract Infections
Seven General Functions of the Respiratory System
Digestive System Anatomy: Diagram, Organs, Structures, and Functions
Kidney Embryology & Development: Easy Lesson
Psychology 101: Crowd Psychology and The Theory of Gustave Le Bon
Introduction to Evolution: Charles Darwin and Alfred Russel Wallace
Copyright © 2022 Moosmosis Organization: All Rights Reserved
All rights reserved. This essay first published on moosmosis.org or any portion thereof may not be reproduced or used in any manner whatsoever
without the express written permission of the publisher at moosmosis.org.

Please Like and Subscribe to our Email List at moosmosis.org, Facebook, Twitter, Youtube to support our open-access youth education initiatives! 🙂












Helpful thanks!
LikeLiked by 1 person
Amazing article on calculus!
LikeLiked by 1 person
Thank you Amy! That’s very nice of you. Happy learning! 🙂
LikeLike