A look at the relationship between limits and the continuity of a function
In the last article, we started talking about limits and their applications for analyzing functions. In this article, we will look at how limits can be used to determine the continuity of a function at a point.
AP Calculus: Learn about Limits and Continuity
So, what exactly does it mean for something to be continuous? Here’s a hint. Look at the 2 graphs below. The one on the left is continuous, but the one on the right is not.

Got it? The one on the left is continuous, because it has no breaks in its graph. Meanwhile, the one on the right is certainly not continuous, because it exhibits several gaps. Though remember, one break in a function’s graph is enough for it to be deemed non-continuous; it is not necessary for it to have multiple gaps.
The continuity of a function can be split into 2 types.
- Continuity on an interval
- Continuity at a point
Continuity on an interval
For a function to be continuous on [a, b], you should be able to draw or trace the function from one endpoint to the other without lifting your pencil. Some easy ways to determine if a function is not continuous on an interval is to look for different types of discontinuities (holes, asymptotes, etc.) which arise when a function is undefined. These can often be easily spotted by looking for:
- Logarithms with arguments that are nonpositive
- Square roots of nonpositive values
- Division by 0
Mathematically speaking, for this to happen every point in the interval must be defined and satisfy the criteria for continuity at a point, which brings us to our second type.
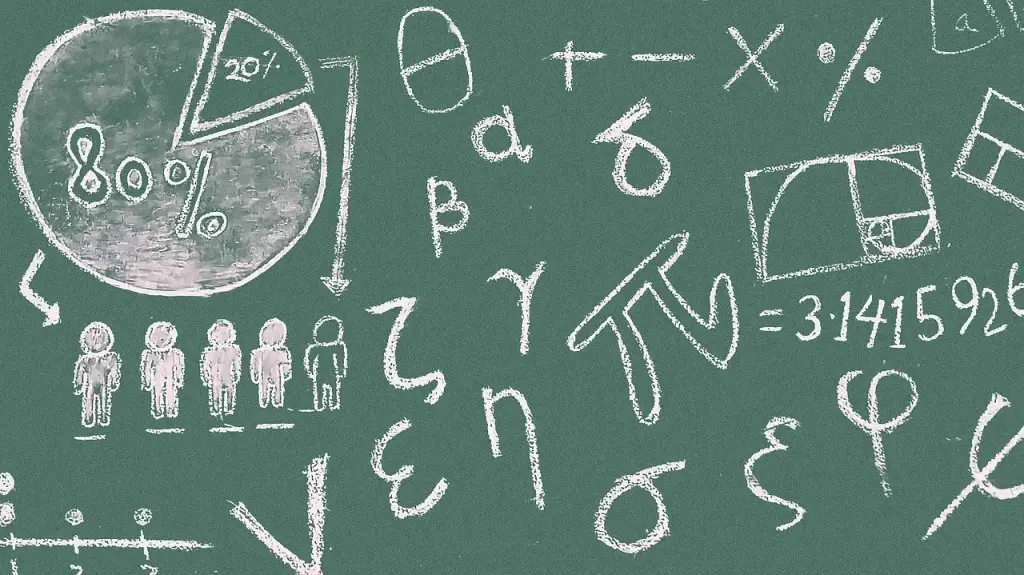
Continuity at a point
Determining continuity at a point requires a little more analysis. To help us determine whether a function is continuous at some value x = c, we think back to our study of limits.
Remember that limits are written as:

Also recall that one-sided limits can be denoted by
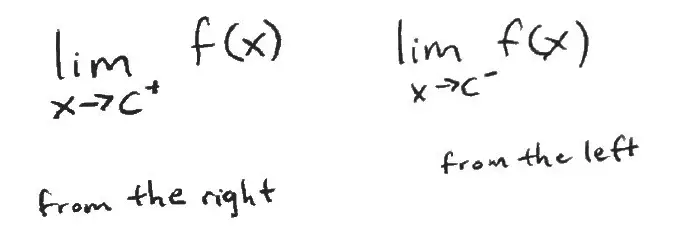
and that if both of these one-sided limits exist and are equal for x = c, then the overall limit of the function as x approaches the value of c exists and is equal to that same value.
Since the graph on the left (above) is continuous, we know that there is continuity at each point on the graph as well. But how could we determine this by just looking at a single point and not the entire function?
First, looking at each x value for which a function is continuous, we notice that the limit always exists. Below is an example of this:

Here, the graph is continuous at x = c; notice that the function approaches the same value from the left and right of c, and thus the limit exists. This is true for all points at which a function is continuous.
Important: for a function to be continuous at x = c, the limit as x approaches c must exist
- This can be tested using one-sided limits
But is this enough to guarantee continuity at a point? NO! To see why, think back to when we learned about limits.
We stated that:

To visualize this, take a look at the graph below:
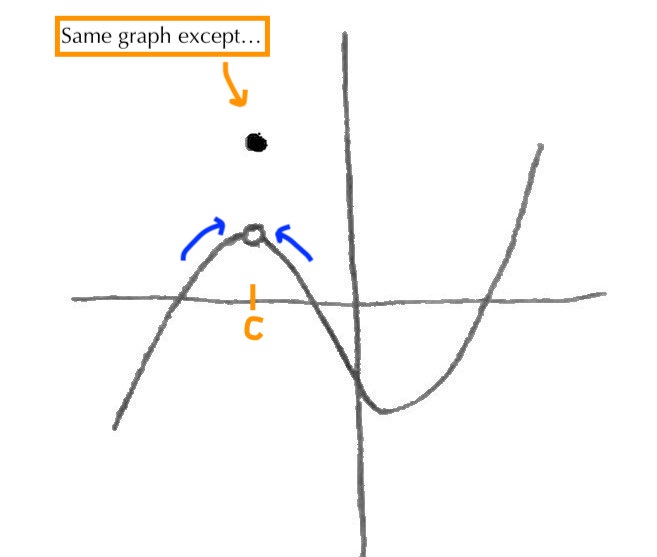
This is the same graph as in the previous example, except now there is a “hole” at x = c. Notice that the limit as x approaches c is still the same; however, our function is not continuous at c as you cannot trace this curve without lifting your pencil. Why is this?
The problem is that the limit at c is not equal to the value of f(c), leading to a gap in the curve. We conclude that even if some function f(x) approaches a certain y-value as x approaches c, if f(c) equals a different y-value (or is not defined) then f(x) is not continuous at x = c.
Important: for a function f(x) to be continuous at x = c, the limit as x approaches c of f(x) must equal f(c)
Putting it all together, we have the criteria for continuity at a point x = c on a function f(x):
Criteria for continuity:

Continuity is important to understand in AP calculus as it often shows up on the AP exam in one form or another. Sometimes you will be asked to determine the continuity of a function at a point using limits, sometimes continuity will play a role in important theorems that you must use (we will look at these in a later chapter), and other times continuity (or rather discontinuities) will be needed as markers for intervals in different function-analysis tests.
Works cited
https://www.sagemath.org/calctut/continuity.html
http://tutorial.math.lamar.edu/Classes/CalcI/Continuity.aspx
http://wmueller.com/precalculus/families/1_31.html
http://sosmath.com/calculus/limcon/limcon05/limcon05.html

© Copyright 2020 Moosmosis – All rights reserved
All rights reserved. This essay or any portion thereof
may not be reproduced or used in any manner whatsoever
without the express written permission of the publisher.

Please Donate and Like our Facebook page to support! 🙂
Categories: education, math, physics, stem, Uncategorized












Great explanation! You make limits so easy to understand which I know can be a hard concept to explain. Thank you! 🙂
https://mathsux.org/
LikeLike
Great article on continuity!
LikeLike
interesting article!
LikeLike
I myself am working on a series for multivariate calculus; it’s nice to look back to the governing principles from time to time. Great article. Look forward to seeing what you put out in the future
LikeLiked by 1 person